LeetCode

LeetCode - BFS广度优先搜索

Posted by SH on October 22, 2020

BFS-广度优先搜索

流程

广度优先搜索使用队列（queue）来实现： 1、把根节点放到队列的末尾。 2、每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。 3、找到所要找的元素时结束程序。 4、如果遍历整个树还没有找到，结束程序。

基本框架

  • 核心思想：抽象成 图 ，从一个点开始，向四周开始扩散。
  • 一般来说，写 BFS 算法都是用 队列 这种数据结构，每次将一个节点周围的所有节点加入队列。
  • BFS 的判断重复如果直接判断十分耗时，一般借助 哈希表 来优化时间复杂度。

BFS框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    // 核心数据结构
    Queue<Node> q; 
    // visited 的主要作用是防止走回头路，大部分时候都是必须的，
    // 但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要 visited
    Set<Node> visited;

    // 将起点加入队列
    q.offer(start); 
    visited.add(start);
    // 记录扩散的步数
    int step = 0;

    while (q not empty) {
        int sz = q.size();
        // 将当前队列中的所有节点向四周扩散
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            // 将 cur 的相邻节点加入队列
            // cur.adj() 泛指 cur 相邻的节点，比如说二维数组中，cur 上下左右四面的位置就是相邻节点
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

题目

102.二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class BinaryTreeLevelOrderTraversal {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new LinkedList<>();
        if (Objects.isNull(root)) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            List<Integer> listLevel = new LinkedList<>();
            int levelSize = queue.size();
            for (int i = 0; i < levelSize; i++) {
                TreeNode cur = queue.poll();
                listLevel.add(cur.val);
                if (!Objects.isNull(cur.left)) {
                    queue.add(cur.left);
                }
                if (!Objects.isNull(cur.right)) {
                    queue.add(cur.right);
                }
            }
            res.add(listLevel);
        }
        return res;
    }
}

103.二叉树的锯齿形层次遍历

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class BinaryTreeZigzagLevelOrderTraversal {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new LinkedList<>();
        if (Objects.isNull(root)) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        // 标志该层遍历方向
        boolean isLeft = true;
        while (!queue.isEmpty()) {
            LinkedList<Integer> listLevel = new LinkedList<>();
            int levelSize = queue.size();
            for (int i = 0; i < levelSize; i++) {
                TreeNode cur = queue.poll();
                // 根据遍历方向采用头插还是尾插
                if (isLeft) {
                    listLevel.add(cur.val);
                } else {
                    listLevel.addFirst(cur.val);
                }
                if (!Objects.isNull(cur.left)) {
                    queue.add(cur.left);
                }
                if (!Objects.isNull(cur.right)) {
                    queue.add(cur.right);
                }
            }
            res.add(listLevel);
            // 方向取反
            isLeft = !isLeft;
        }
        return res;
    }
}

111.二叉树的最小深度

给定一个二叉树，找出其最小深度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class MinimumDepthOfBinaryTree {
    public int minDepth(TreeNode root) {
        int res = 0;
        if (root == null) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                // 叶子节点
                if (cur.left == null && cur.right == null) {
                    return res + 1;
                }
                if (cur.left != null) {
                    queue.add(cur.left);
                }
                if (cur.right != null) {
                    queue.add(cur.right);
                }
            }
            res++;
        }
        return res;
    }
}

200.岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。 岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。 此外，你可以假设该网格的四条边均被水包围。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class NumberOfIslands {
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }
        int num = 0;
        int h = grid.length;
        int w = grid[0].length;
        boolean[][] visited = new boolean[h][w];
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                if (grid[i][j] == '1' && !visited[i][j]) {
                    num++;
                    visited[i][j] = true;
                    Queue<Integer> queue = new LinkedList<>();
                    queue.add(i * w + j);
                    while (!queue.isEmpty()) {
                        // 当前位置
                        int cur = queue.poll();
                        int row = cur / w;
                        int col = cur % w;
                        // 当前位置4个方向遍历
                        if (row - 1 >= 0 && grid[row - 1][col] == '1' && !visited[row - 1][col]) {
                            queue.add((row - 1) * w + col);
                            visited[row - 1][col] = true;
                        }
                        if (row + 1 < h && grid[row + 1][col] == '1' && !visited[row + 1][col]) {
                            queue.add((row + 1) * w + col);
                            visited[row + 1][col] = true;
                        }
                        if (col - 1 >= 0 && grid[row][col - 1] == '1' && !visited[row][col - 1]) {
                            queue.add(row * w + col - 1);
                            visited[row][col - 1] = true;
                        }
                        if (col + 1 < w && grid[row][col + 1] == '1' && !visited[row][col + 1]) {
                            queue.add(row * w + col + 1);
                            visited[row][col + 1] = true;
                        }
                    }
                }
            }
        }
        return num;
    }
}

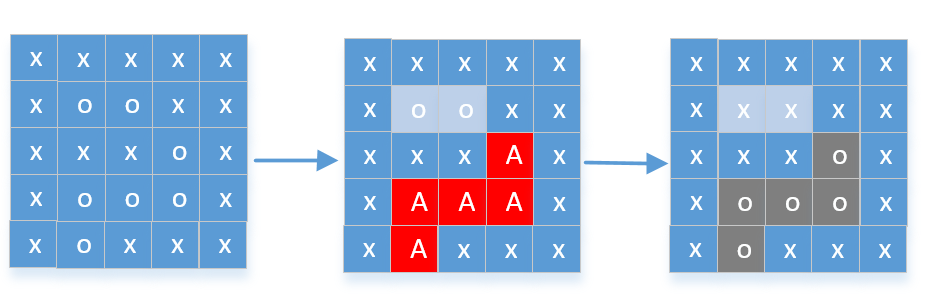
130.被围绕的区域

给定一个二维的矩阵，包含 ‘X’ 和 ‘O’（字母 O）。 找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

image.png

题解-DFS和BFS两种方式解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

class SurroundedRegions {
    public void solve(char[][] board) {
        if (board == null || board.length == 0) {
            return;
        }
        int h = board.length;
        int w = board[0].length;
        boolean[][] visited = new boolean[h][w];
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                if (board[i][j] == 'O' && !visited[i][j]) {
                    board[i][j] = 'X';
                    visited[i][j] = true;
                    Queue<int[]> queue = new LinkedList<>();
                    queue.add(new int[]{i, j});
                    // 记录当前一次遍历位置，用于还原
                    List<int[]> tmpVisited = new LinkedList<>();
                    tmpVisited.add(new int[]{i, j});
                    boolean flag = false;
                    while (!queue.isEmpty()) {
                        int[] cur = queue.poll();
                        int row = cur[0];
                        int col = cur[1];
                        // 边界判断
                        if (row == 0 || row == h - 1 || col == 0 || col == w - 1) {
                            flag = true;
                        }
                        // 当前位置4个方向遍历
                        if (row - 1 >= 0 && board[row - 1][col] == 'O' && !visited[row - 1][col]) {
                            queue.add(new int[]{row - 1, col});
                            tmpVisited.add(new int[]{row - 1, col});
                            visited[row - 1][col] = true;
                            board[row - 1][col] = 'X';
                        }
                        if (row + 1 < h && board[row + 1][col] == 'O' && !visited[row + 1][col]) {
                            queue.add(new int[]{row + 1, col});
                            tmpVisited.add(new int[]{row + 1, col});
                            visited[row + 1][col] = true;
                            board[row + 1][col] = 'X';
                        }
                        if (col - 1 >= 0 && board[row][col - 1] == 'O' && !visited[row][col - 1]) {
                            queue.add(new int[]{row, col - 1});
                            tmpVisited.add(new int[]{row, col - 1});
                            visited[row][col - 1] = true;
                            board[row][col - 1] = 'X';
                        }
                        if (col + 1 < w && board[row][col + 1] == 'O' && !visited[row][col + 1]) {
                            queue.add(new int[]{row, col + 1});
                            tmpVisited.add(new int[]{row, col + 1});
                            visited[row][col + 1] = true;
                            board[row][col + 1] = 'X';
                        }
                    }
                    // 如果超过边界，还原board
                    if (flag) {
                        for (int[] t : tmpVisited) {
                            board[t[0]][t[1]] = 'O';
                        }
                    }
                }
            }
        }
    }


    public void solve2(char[][] board) {
        if (board == null || board.length == 0) {
            return;
        }
        int h = board.length;
        int w = board[0].length;
        Queue<int[]> queue = new LinkedList<>();
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                // 判断边缘的’O‘
                if (board[i][j] == 'O' && (i == 0 || i == h - 1 || j == 0 || j == w - 1)) {
                    // 将边缘的’O‘置为’T‘标识，然后BFS遍历所有相连的’O‘都置为’T‘
                    board[i][j] = 'T';
                    queue.add(new int[]{i, j});
                    while (!queue.isEmpty()) {
                        int[] cur = queue.poll();
                        int row = cur[0];
                        int col = cur[1];
                        // BFS四个方向的’O‘
                        if (row - 1 >= 0 && board[row - 1][col] == 'O') {
                            queue.add(new int[]{row - 1, col});
                            board[row - 1][col] = 'T';
                        }
                        if (row + 1 < h && board[row + 1][col] == 'O') {
                            queue.add(new int[]{row + 1, col});
                            board[row + 1][col] = 'T';
                        }
                        if (col - 1 >= 0 && board[row][col - 1] == 'O') {
                            queue.add(new int[]{row, col - 1});
                            board[row][col - 1] = 'T';
                        }
                        if (col + 1 < w && board[row][col + 1] == 'O') {
                            queue.add(new int[]{row, col + 1});
                            board[row][col + 1] = 'T';
                        }
                    }
                }
            }
        }
        // 所有与边缘相连的’O‘都被置为了’T‘，剩余的’O‘都是中间被’X‘包围的
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                } else if (board[i][j] == 'T') {
                    board[i][j] = 'O';
                }
            }
        }
    }
}

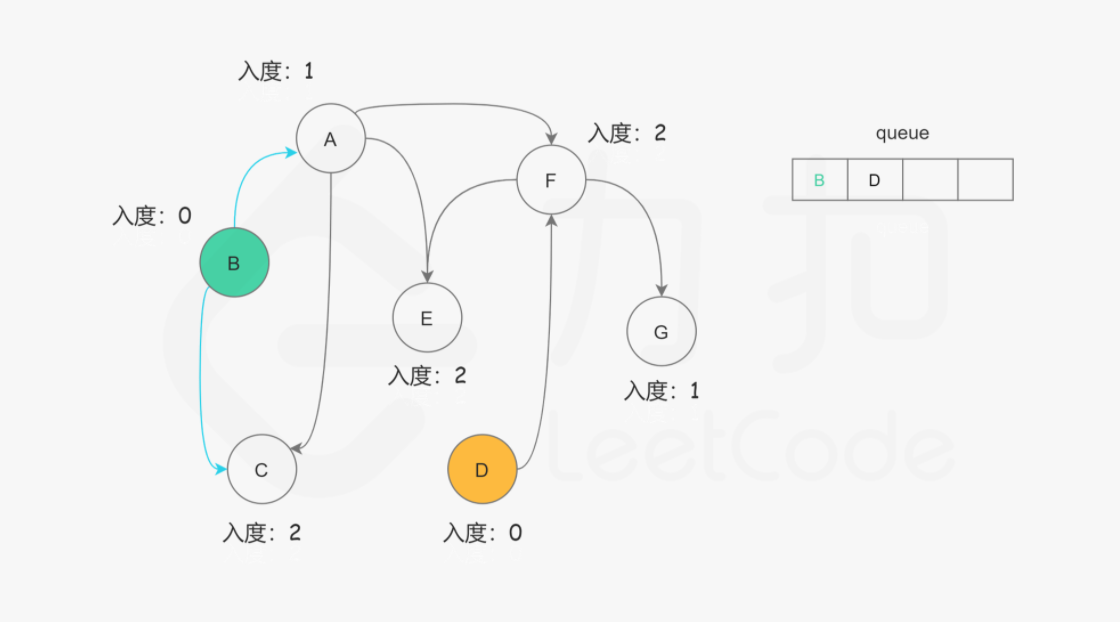
207.课程表

你这个学期必须选修 numCourse 门课程，记为 0 到 numCourse-1 。 在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们：[0,1] 给定课程总量以及它们的先决条件，请你判断是否可能完成所有课程的学习？

image-20201022204603570

题解-官方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class N0207CourseSchedule {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 当前课程为先修课程的后续课程链表（邻接表）
        List<List<Integer>> edges = new ArrayList<>();
        // 每门课程的先修课程数量（入度）
        int[] indeg = new int[numCourses];
        for (int i = 0; i < numCourses; i++) {
            edges.add(new LinkedList<>());
        }
        for (int[] p : prerequisites) {
            edges.get(p[1]).add(p[0]);
            indeg[p[0]]++;
        }
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            // 入度为0（无需先修课程的课程）
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }
        int visited = 0;
        while (!queue.isEmpty()) {
            visited++;
            int pre = queue.poll();
            // 遍历以当前课程为先修课程的后续课程链表
            for (int cur : edges.get(pre)) {
                indeg[cur]--;
                // 如果入度（先修课程数量）为0，加入队列
                if (indeg[cur] == 0) {
                    queue.offer(cur);
                }
            }
        }
        return visited == numCourses;
    }
}

127.单词接龙

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。 转换需遵循如下规则： 每次转换只能改变一个字母。 转换过程中的中间单词必须是字典中的单词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

class WordLadder {
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        if (beginWord.equals(endWord)) {
            return 1;
        }
        // 将wordList转wordSet，不转Set直接用wordList.contains()判断会超时
        Set<String> wordSet = new HashSet<>(wordList);
        if (wordSet.isEmpty() || !wordSet.contains(endWord)) {
            return 0;
        }
        wordSet.remove(beginWord);

        Queue<String> queue = new LinkedList<>();
        queue.offer(beginWord);
        Set<String> visited = new HashSet<>();
        visited.add(beginWord);

        int res = 0;
        int wordLength = beginWord.length();
        while (!queue.isEmpty()) {
            res++;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                String curWord = queue.poll();
                char[] charArray = curWord.toCharArray();
                for (int j = 0; j < wordLength; j++) {
                    char curChar = curWord.charAt(j);
                    for (char k = 'a'; k <= 'z'; k++) {
                        if (k == curChar) {
                            continue;
                        }
                        // 替换一个字符
                        charArray[j] = k;
                        String nextWord = String.valueOf(charArray);
                        if (wordSet.contains(nextWord)) {
                            if (nextWord.equals(endWord)) {
                                return res + 1;
                            }
                            if (!visited.contains(nextWord)) {
                                queue.offer(nextWord);
                                visited.add(nextWord);
                            }
                        }
                    }
                    // 恢复
                    charArray[j] = curChar;
                }
            }
        }
        return 0;
    }
}

126.单词接龙 II

给定两个单词（beginWord 和 endWord）和一个字典 wordList，找出所有从 beginWord 到 endWord 的最短转换序列。 转换需遵循如下规则： 每次转换只能改变一个字母。 转换后得到的单词必须是字典中的单词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

class WordLadder2 {
    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
        List<List<String>> res = new LinkedList<>();
        // 将wordList转wordSet，不转Set直接用wordList.contains()判断会超时
        Set<String> wordSet = new HashSet<>(wordList);
        if (wordSet.isEmpty() || !wordSet.contains(endWord)) {
            return res;
        }
        wordSet.remove(beginWord);

        // 队列存储所有转换序列
        Queue<List<String>> queue = new LinkedList<>();
        List<String> beginPath = new LinkedList<>();
        beginPath.add(beginWord);
        queue.offer(beginPath);
        // 已访问的单词
        Set<String> visited = new HashSet<>();
        visited.add(beginWord);

        int wordLength = beginWord.length();
        while (!queue.isEmpty()) {
            int size = queue.size();
            // 该层已访问的
            Set<String> subVisited = new HashSet<>();
            for (int i = 0; i < size; i++) {
                List<String> curPath = queue.poll();
                // 序列最后一个单词
                String curWord = curPath.get(curPath.size() - 1);
                char[] charArray = curWord.toCharArray();
                for (int j = 0; j < wordLength; j++) {
                    char curChar = curWord.charAt(j);
                    for (char k = 'a'; k <= 'z'; k++) {
                        if (k == curChar) {
                            continue;
                        }
                        // 替换一个字符
                        charArray[j] = k;
                        String nextWord = String.valueOf(charArray);
                        if (wordSet.contains(nextWord) && !visited.contains(nextWord)) {
                            if (nextWord.equals(endWord)) {
                                curPath.add(nextWord);
                                res.add(new ArrayList<>(curPath));
                                curPath.remove(curPath.size() - 1);
                            }
                            curPath.add(nextWord);
                            queue.offer(new ArrayList<>(curPath));
                            curPath.remove(curPath.size() - 1);
                            subVisited.add(nextWord);
                        }
                    }
                    // 恢复
                    charArray[j] = curChar;
                }
            }
            visited.addAll(subVisited);
        }
        return res;
    }
}

双向 BFS

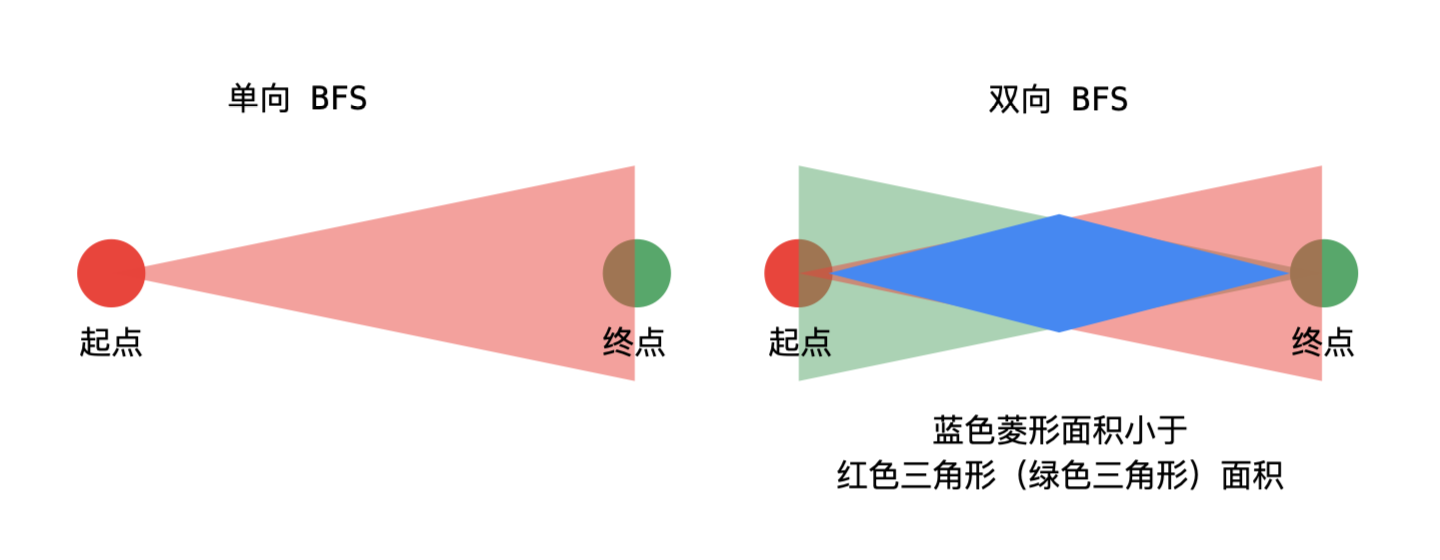
双向广度优先遍历

  • 传统的 BFS 框架就是从起点开始向四周扩散，遇到终点时停止。
  • 双向 BFS 则是从起点和终点同时开始扩散，当两边有交集的时候停止。
  • 双向 BFS 还是遵循 BFS 算法框架的，只是不再使用队列，而是使用 HashSet 方便快速判断两个集合是否有交集。
  • 双向 BFS 也有局限，必须知道终点在哪里。

trick

  • while 循环的最后交换 q1 和 q2 的内容，所以只要默认扩散 q1 就相当于轮流扩散 q1 和 q2。
  • while 循环开始时根据 q1 和 q2 的大小进行交换。
1
2
3
4
5
6
7
8
9

// ...
while (!q1.isEmpty() && !q2.isEmpty()) {
    if (q1.size() > q2.size()) {
        // 交换 q1 和 q2
        temp = q1;
        q1 = q2;
        q2 = temp;
    }
    // ...

无论传统 BFS 还是双向 BFS，无论做不做优化，从 Big O 衡量标准来看，时间复杂度都是一样的， 只能说双向 BFS 是一种 trick，算法运行的速度会相对快一点。

127.单词接龙

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

class WordLadder {
    /*双向BFS*/
    public int ladderLength2(String beginWord, String endWord, List<String> wordList) {
        // 将wordList转wordSet，不转Set直接用wordList.contains()判断会超时
        Set<String> wordSet = new HashSet<>(wordList);
        if (wordSet.isEmpty() || !wordSet.contains(endWord)) {
            return 0;
        }
        wordSet.remove(beginWord);

        Set<String> visited = new HashSet<>();
        // 用开始结束两边的哈希表代替单向 BFS 里的队列
        Set<String> beginVisited = new HashSet<>();
        beginVisited.add(beginWord);
        Set<String> endVisited = new HashSet<>();
        endVisited.add(endWord);

        int res = 0;
        int wordLength = beginWord.length();
        while (!beginVisited.isEmpty() && !endVisited.isEmpty()) {
            res++;
            // 比较大小交换，优先选择小的哈希表进行扩散
            if (beginVisited.size() > endVisited.size()) {
                Set<String> tmp = beginVisited;
                beginVisited = endVisited;
                endVisited = tmp;
            }
            // nextLevelVisited 在扩散完成以后，会成为新的 beginVisited
            Set<String> nextLevelVisited = new HashSet<>();
            for (String curWord : beginVisited) {
                char[] charArray = curWord.toCharArray();
                for (int j = 0; j < wordLength; j++) {
                    char curChar = curWord.charAt(j);
                    for (char k = 'a'; k <= 'z'; k++) {
                        if (k == curChar) {
                            continue;
                        }
                        // 替换一个字符
                        charArray[j] = k;
                        String nextWord = String.valueOf(charArray);
                        if (wordSet.contains(nextWord)) {
                            // 前后相交
                            if (endVisited.contains(nextWord)) {
                                return res + 1;
                            }
                            if (!visited.contains(nextWord)) {
                                nextLevelVisited.add(nextWord);
                                visited.add(nextWord);
                            }
                        }
                    }
                    // 恢复
                    charArray[j] = curChar;
                }
            }
            beginVisited = nextLevelVisited;
        }
        return 0;
    }
}

References

CATALOG
    FEATURED TAGS
    Linux BBigData CSAPP LeetCode TOUR TensorFlow HADOOP Spark Java Kafka Kubernetes
    FRIENDS